Dados são um dos temas que mais atraem atenção atualmente. À medida que os processos se tornam cada vez mais digitalizados na sociedade, maior é o volume de dados coletados e o desafio de transformá-los em informações úteis.
Neste contexto, conhecimentos relativos à visualização e modelagem de dados podem ser fundamentais para a melhoria de processos e de tomada de decisão. De modo que podem tornar o fluxo de trabalho mais eficiente em qualquer área de conhecimento.
Anteriormente, exploramos um pouco essa possibilidade no cenário imaginário no qual aplicamos o método AHP para a escolha de um novo produto alimentício. No texto de hoje vamos ilustrar este potencial explorando um famoso dataset na análise de dados, o Iris.
A partir dessas medidas, pode ser interessante investigar se as dimensões de sépala e pétala são relevantes para diferenciar as flores Iris entre si, por exemplo. Contudo, antes de investir energia nesta questão, é necessário conhecer melhor os dados disponíveis para saber se sequer é possível explorar este problema a partir das informações disponíveis.
Normalmente, a preocupação inicial ao trabalhar com um banco de dados desconhecido é a qualidade dos registros: quantidade de valores faltantes, tipos e escala das variáveis e dispersão das observações. No caso do Iris, não será necessário tratar o primeiro problema, uma vez que todas as linhas estão devidamente preenchidas. Todavia, é útil saber como os valores estão espalhados.
Como é mostrado na Figura 1, o nosso dataset possui 4 variáveis quantitativas contínuas: comprimento da sépala, largura da sépala, comprimento da pétala e largura da pétala. Para cada uma delas, é possível obter estatísticas de tendência central como a média, a mediana e a média truncada (média obtida após a retirada dos valores mais extremos da variável).
A Figura 2 apresenta os valores dessas estatísticas para cada uma dessas medidas, considerando um corte de 20% dos menores e maiores valores para cálculo da média truncada.
A avaliação destas três medidas em conjunto podem dar uma noção da presença de outliers. Caso os resultados sejam muito diferentes entre si, há um forte indício da influência de valores extremos nas estatísticas.
No entanto, pode ser mais interessante detectar outliers a partir de medidas de espalhamento. Algumas dessas medidas são: range, variância (s²), desvio médio absoluto (AAD), desvio mediano absoluto (MAD) e o intervalo interquartil (IQR). A definição de cada uma delas é apresentada a seguir:
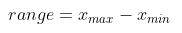
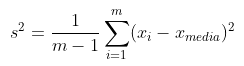
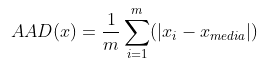
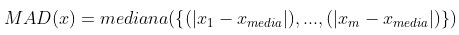
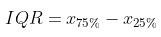
Neste contexto, conhecimentos relativos à visualização e modelagem de dados podem ser fundamentais para a melhoria de processos e de tomada de decisão. De modo que podem tornar o fluxo de trabalho mais eficiente em qualquer área de conhecimento.
 |
| (Imagem de pixabay) |
Anteriormente, exploramos um pouco essa possibilidade no cenário imaginário no qual aplicamos o método AHP para a escolha de um novo produto alimentício. No texto de hoje vamos ilustrar este potencial explorando um famoso dataset na análise de dados, o Iris.
Conhecendo os dados
O Iris consiste em um banco de dados com 150 observações. Para cada registro, são informados comprimento e largura da sépala e da pétala das flores Iris setosa, Iris versicolor e Iris virginica. A Figura 1 apresenta a estrutura da disposição desses dados.| Figura 1: Estrutura do Iris. |
A partir dessas medidas, pode ser interessante investigar se as dimensões de sépala e pétala são relevantes para diferenciar as flores Iris entre si, por exemplo. Contudo, antes de investir energia nesta questão, é necessário conhecer melhor os dados disponíveis para saber se sequer é possível explorar este problema a partir das informações disponíveis.
Normalmente, a preocupação inicial ao trabalhar com um banco de dados desconhecido é a qualidade dos registros: quantidade de valores faltantes, tipos e escala das variáveis e dispersão das observações. No caso do Iris, não será necessário tratar o primeiro problema, uma vez que todas as linhas estão devidamente preenchidas. Todavia, é útil saber como os valores estão espalhados.
Como é mostrado na Figura 1, o nosso dataset possui 4 variáveis quantitativas contínuas: comprimento da sépala, largura da sépala, comprimento da pétala e largura da pétala. Para cada uma delas, é possível obter estatísticas de tendência central como a média, a mediana e a média truncada (média obtida após a retirada dos valores mais extremos da variável).
A Figura 2 apresenta os valores dessas estatísticas para cada uma dessas medidas, considerando um corte de 20% dos menores e maiores valores para cálculo da média truncada.
| Figura 2: média truncada, média e mediana para variáveis numéricas do Iris. |
A avaliação destas três medidas em conjunto podem dar uma noção da presença de outliers. Caso os resultados sejam muito diferentes entre si, há um forte indício da influência de valores extremos nas estatísticas.
No entanto, pode ser mais interessante detectar outliers a partir de medidas de espalhamento. Algumas dessas medidas são: range, variância (s²), desvio médio absoluto (AAD), desvio mediano absoluto (MAD) e o intervalo interquartil (IQR). A definição de cada uma delas é apresentada a seguir:
Na Figura 3, cada uma dessas medidas são apresentadas. Perceba que a análise destas estatísticas em conjunto permite uma visão mais robusta do espalhamento de dados, uma vez que se dilui a influência da média, uma estatística sensível a outliers, nos resultados.
| Figura 3: range, variância, AAD, MAD e IQR para as variáveis numéricas do Iris. |
Lembre-se que o espalhamento não é somente sobre o quão distantes estão os valores mais altos dos menores, mas também sobre a distribuição da maioria dos dados. Na Figura 3, por exemplo, observa-se que apesar de possuírem o mesmo range, sepal width (largura da sépala) possui os dados concentrados em uma faixa significativamente menor do que petal width (largura da pétala).
Apesar de serem referências úteis para a análise da dispersão dos dados, muitas vezes a análise gráfica pode te dar uma noção muito mais confiante do comportamento das variáveis. Uma visualização muito comum para este objetivo é o box-plot, com o qual você deve se deparar em algum momento da graduação.
Os box-plots para as variáveis numéricas do Iris estão apresentados na Figura 4. Na imagem, é possível notar imediatamente a presença de outliers para a largura da sépala. Algo que não seria possível perceber com tanta facilidade avaliando somente os estimadores numéricos apresentados.
Ainda tentando conhecer melhor as características das variáveis de trabalho, podemos ter interesse na distribuição de cada uma delas. Uma forma simples de fazer este tipo de análise é a partir dos histogramas. A Figura 5a apresenta o histograma para a variável sepal width, na Figura 5b temos o mesmo tipo de gráfico para petal length (comprimento da pétala).
Por fim, devemos olhar para a variável categórica class (classe). Começamos o texto propondo utilizar o Iris para entender se as dimensões da sépala e da pétala são relevantes para a diferenciação das flores.
Para sabermos se é possível (ou aconselhável) fazer esta investigação, precisamos saber quantas observações para cada tipo de flor estão disponíveis no banco de dados. Afinal, caso um tipo de flor esteja muito mais documentado do que os demais, a qualidade da análise fica comprometida devido à falta de dados registrados para as outras classes.
A verificação da quantidade de registro por flor pode ser feita a partir da construção de uma tabela de frequência para a variável class. Esta tabela é apresentada na Figura 6.
Na Figura 6 estão as quantidades de ocorrências para cada uma das flores registradas no Iris. Vemos que, neste caso, as 150 observações se dividem igualmente entre cada planta. Para datasets mais complexos, este nem sempre será o caso.
Neste contexto, entra a análise multivariada. Na Figura 7 é apresentado um mapa de calor ou densidade (ou ainda, histograma 2D) para as variáveis petal length e petal width (largura da pétala) do Iris.
Neste histograma, são mostradas a quantidade de ocorrências das observações que são compatíveis com duas condições em comum. Por exemplo, no dataset há 37 plantas documentadas cujo comprimento da pétala está entre 4 cm e 5,9 cm e a largura da pétala está entre 1,3 cm e 1,7 cm. Por outro lado, não há nenhuma flor com pétala entre 6 cm e 7,9 cm de comprimento e 0,3 cm a 0,7 cm de largura.
Este mapa de calor, sugere que as combinações de valores possíveis para os atributos é limitada, e que há mais ocorrências para determinadas faixas do que outras. Esta característica não seria percebida a partir do uso de nenhuma das estratégias de análise e visualização de dados que exploramos até aqui.
Outro gráfico muito utilizado para a análise multivariada é o gráfico de dispersão. Muito comum em trabalhos científicos, certamente você já teve que trabalhar com este tipo de gráfico durante a elaboração de algum relatório.
Na Figura 8, é apresentada a matriz de gráficos de dispersão para as variáveis do Iris. Nela, é possível ver a relação entre as variáveis contínuas, além de ser possível notar, visualmente, que, de fato, os pontos associados a cada tipo de flor tendem a se aglomerar em regiões diferentes do gráfico para alguns pares de variáveis.
Relembrando o problema proposto inicialmente neste texto, a Figura 8 é uma evidência visual de que as dimensões de sépala e pétala podem ser relevantes para diferenciar um tipo de flor de outro. Nela também é possível observar que os pontos associados à Iris-setosa tendem a se destacar dos demais, enquanto Iris-versicolor e Iris-virginica estão mais próximas e até se misturam para alguns pares de variáveis.
A evidência apresentada pela Figura 8 pode ser confirmada a partir de uma técnica chamada discretização. A discretização é uma forma de simplificar a análise de dados contínuos. Para este exemplo, podemos selecionar as variáveis petal width e petal length para a discretização e fazer as seguintes substituições:
De acordo com a tabela, 100% das flores Iris-setosa presentes no dataset possuem pétala com comprimento de até 2,5 cm e largura de até 0,75 cm. Também notamos que não foi registrado um comprimento de pétala nesta faixa para nenhum dos outros tipos de flor.
As frequências apresentadas indicam que valores medianos comumente são encontrados para flores Iris-versicolor, enquanto valores mais altos estão associados a Iris-virginica. Como foi visto nos gráficos de dispersão, entretanto, os dados para estas duas flores estão mais próximos, de modo que há algumas ocorrências de dimensões altas para a Iris versicolor e de dimensões medianas para a Iris virginica.
A partir deste tipo de regressão, constrói-se um modelo matemático que permite classificar se uma observação é referente à Iris-setosa, Iris-versicolor ou Iris-virginica de acordo com os tamanhos de sépala e pétala. Você pode dar uma olhada em como seria este processo em Python clicando aqui.
Todas as visualizações, estimadores e técnica de discretização apresentados neste texto foram feitos seguindo o capítulo Exploring Data, disponível neste link. O código para a construção de cada uma destas etapas em Python pode ser acessado aqui.
Apesar de serem referências úteis para a análise da dispersão dos dados, muitas vezes a análise gráfica pode te dar uma noção muito mais confiante do comportamento das variáveis. Uma visualização muito comum para este objetivo é o box-plot, com o qual você deve se deparar em algum momento da graduação.
Os box-plots para as variáveis numéricas do Iris estão apresentados na Figura 4. Na imagem, é possível notar imediatamente a presença de outliers para a largura da sépala. Algo que não seria possível perceber com tanta facilidade avaliando somente os estimadores numéricos apresentados.
| Figura 4: box-plots de sepal length, sepal width, petal length e petal width. |
| Figura 5a: Distribuição da largura da sépala. |
| Figura 5b: Distribuição do comprimento da pétala. |
Por fim, devemos olhar para a variável categórica class (classe). Começamos o texto propondo utilizar o Iris para entender se as dimensões da sépala e da pétala são relevantes para a diferenciação das flores.
Para sabermos se é possível (ou aconselhável) fazer esta investigação, precisamos saber quantas observações para cada tipo de flor estão disponíveis no banco de dados. Afinal, caso um tipo de flor esteja muito mais documentado do que os demais, a qualidade da análise fica comprometida devido à falta de dados registrados para as outras classes.
A verificação da quantidade de registro por flor pode ser feita a partir da construção de uma tabela de frequência para a variável class. Esta tabela é apresentada na Figura 6.
| Figura 6: Tabela de frequência de classe. |
Na Figura 6 estão as quantidades de ocorrências para cada uma das flores registradas no Iris. Vemos que, neste caso, as 150 observações se dividem igualmente entre cada planta. Para datasets mais complexos, este nem sempre será o caso.
Aprofundando-se na visualização de dados
Apesar de já conhecermos algumas estatísticas básicas do banco de dados, até agora não exportamos nenhuma das descobertas feitas para a área de conhecimento interessada nas características dessas plantas. Para que isso seja possível, é necessária uma análise mais profunda das variáveis apresentadas.Neste contexto, entra a análise multivariada. Na Figura 7 é apresentado um mapa de calor ou densidade (ou ainda, histograma 2D) para as variáveis petal length e petal width (largura da pétala) do Iris.
| Figura 7: Mapa de calor ou densidade de largura da pétala vs comprimento da pétala. |
Neste histograma, são mostradas a quantidade de ocorrências das observações que são compatíveis com duas condições em comum. Por exemplo, no dataset há 37 plantas documentadas cujo comprimento da pétala está entre 4 cm e 5,9 cm e a largura da pétala está entre 1,3 cm e 1,7 cm. Por outro lado, não há nenhuma flor com pétala entre 6 cm e 7,9 cm de comprimento e 0,3 cm a 0,7 cm de largura.
Este mapa de calor, sugere que as combinações de valores possíveis para os atributos é limitada, e que há mais ocorrências para determinadas faixas do que outras. Esta característica não seria percebida a partir do uso de nenhuma das estratégias de análise e visualização de dados que exploramos até aqui.
Outro gráfico muito utilizado para a análise multivariada é o gráfico de dispersão. Muito comum em trabalhos científicos, certamente você já teve que trabalhar com este tipo de gráfico durante a elaboração de algum relatório.
Na Figura 8, é apresentada a matriz de gráficos de dispersão para as variáveis do Iris. Nela, é possível ver a relação entre as variáveis contínuas, além de ser possível notar, visualmente, que, de fato, os pontos associados a cada tipo de flor tendem a se aglomerar em regiões diferentes do gráfico para alguns pares de variáveis.
| Figura 8: Matriz de gráficos de dispersão para as variáveis contínuas do Iris. |
Relembrando o problema proposto inicialmente neste texto, a Figura 8 é uma evidência visual de que as dimensões de sépala e pétala podem ser relevantes para diferenciar um tipo de flor de outro. Nela também é possível observar que os pontos associados à Iris-setosa tendem a se destacar dos demais, enquanto Iris-versicolor e Iris-virginica estão mais próximas e até se misturam para alguns pares de variáveis.
A evidência apresentada pela Figura 8 pode ser confirmada a partir de uma técnica chamada discretização. A discretização é uma forma de simplificar a análise de dados contínuos. Para este exemplo, podemos selecionar as variáveis petal width e petal length para a discretização e fazer as seguintes substituições:
- Se petal width estiver entre 0 e 0,75 -> low;
- Se petal width estiver entre 0,75 e 1,75 -> medium;
- Se petal width > 1,75 -> high;
- Se petal length estiver entre 0 e 2,5 -> low;
- Se petal length estiver entre 2,5 e 5,0 -> medium;
- Se petal length > 5,0 -> high;
| Figura 9: Distribuição dos tipos de flores por intervalos discretizados e petal length e petal width. |
De acordo com a tabela, 100% das flores Iris-setosa presentes no dataset possuem pétala com comprimento de até 2,5 cm e largura de até 0,75 cm. Também notamos que não foi registrado um comprimento de pétala nesta faixa para nenhum dos outros tipos de flor.
As frequências apresentadas indicam que valores medianos comumente são encontrados para flores Iris-versicolor, enquanto valores mais altos estão associados a Iris-virginica. Como foi visto nos gráficos de dispersão, entretanto, os dados para estas duas flores estão mais próximos, de modo que há algumas ocorrências de dimensões altas para a Iris versicolor e de dimensões medianas para a Iris virginica.
Vá além com a Ciência de Dados
Note que, com base na aplicação de técnicas relativamente simples de visualização de dados, foi possível identificar um padrão sobre a relação das dimensões de pétala e sépala e cada uma das três espécies de flores estudadas para os dados disponíveis no Iris. Caso você queira explorar esta relação de maneira ainda mais sofisticada, uma possibilidade é a aplicação de um modelo de regressão logística multinomial sobre o banco de dados.A partir deste tipo de regressão, constrói-se um modelo matemático que permite classificar se uma observação é referente à Iris-setosa, Iris-versicolor ou Iris-virginica de acordo com os tamanhos de sépala e pétala. Você pode dar uma olhada em como seria este processo em Python clicando aqui.
Todas as visualizações, estimadores e técnica de discretização apresentados neste texto foram feitos seguindo o capítulo Exploring Data, disponível neste link. O código para a construção de cada uma destas etapas em Python pode ser acessado aqui.
Note que, enquanto o Iris é uma alternativa simples para começarmos a conhecer mais sobre análise e visualização de dados, na engenharia química bancos muito mais desafiadores podem aparecer. Pode ser necessário, por exemplo, que entendamos profundamente um processo para que possamos entender o significado das variáveis antes mesmo de começarmos a explorar o dataset. Nestes casos, o uso de ferramentas da qualidade, como os fluxogramas, podem fazer toda a diferença para o seu trabalho.
Se você se interessou pela análise de dados e gostaria de se aprofundar no assunto, você pode conhecer mais do trabalho dos autores cujo capítulo inspirou este post aqui. Independente de qual o seu ramo de trabalho, tenho certeza de que entender mais do assunto fará toda a diferença na sua carreira!
Gostou? Confira também:
Se você se interessou pela análise de dados e gostaria de se aprofundar no assunto, você pode conhecer mais do trabalho dos autores cujo capítulo inspirou este post aqui. Independente de qual o seu ramo de trabalho, tenho certeza de que entender mais do assunto fará toda a diferença na sua carreira!
Gostou? Confira também:

Comentários
Postar um comentário
Se chegou até aqui, não deixa de compartilhar com a gente o que você achou!